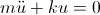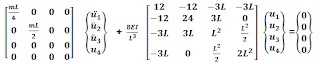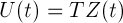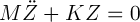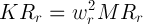On the vibration analysis of MDOF systems

1. Introduction

Equations of motion for multi degree of freedom (MDOF) systems are generally coupled. Coupling between co-ordinates is manifest in the form of structural matrices being non-diagonal. Coupling is not an intrinsic property of a vibrating system. It is dependent upon the choice of the coordinate system. This choice itself is arbitrary. Equations of motion are not unique. They depend upon the choice of coordinate system.

The best choice of coordinate system is the one in which the coupling is absent. That is, the structural matrices are all diagonal. These coordinates are called the natural coordinates for the system. Determination of these coordinates for a given system constitutes a major theme in structural dynamics. Theory of ODEs and linear algebra help us in this aspect.

This write up discusses in detail the solution of the equation of MDOF systems through an example of a cantilever beam.

The following paragraphs comprise of a set of 7 steps which detail/describe the various stages in the solution of the equation of motion of a multi degree of freedom system.

A cantilever beam with 4 degree of freedoms is considererd as an example.

2. Solution of the equation of motion of multi degree of freedom systems

Let us consider a massless cantilever beam with two lumped masses at the mid-point and at the free end as shown in the figure 1 below:

Figure 1: Cantilever beam with lumped mass

Let us first formulate the equation of motion for the beam in figure 1

Step 1: Generation of the mass matrix

With the degrees of freedom defined at the location of the lumped masses we have the diagonal mass matrix given by;

Step 2: Generation of the stiffness matrix

We get the stiffness coefficients by the direct equilibrium method as shown below;

a) To get the first column of the stiffness matrix we impose u1 = 1 and u2=u3=u4=0

The corresponding stiffness coefficients are;

b) To get the second column of the stiffness matrix we impose u2 = 1 and u1=u3=u4=0

The corresponding stiffness coefficients are:

c) To get the third column of the stiffness matrix we impose u3 = 1 and u1=u4=u2=0

The corresponding stiffness coefficients are:

d)To get the third column of the stiffness matrix we impose u4 = 1 and u1=u2=u3=0

The corresponding stiffness coefficients are:

With all the stiffness coefficients determined, the stiffness matrix is given by:

Step 3: Equation of motion for the MDOF (here 4 dof) system:

That is;

Step 4: Carrying out the coordinate transformation:

As seen above the ‘’K” is non diagonal. M is diagonal as it has been assumed in the problem that masses are lumped at nodes.

Therefore this equation of motion is coupled: that is the equations obtained after expanding rhe matric are interdependent and each equation cannot be solved independently,

Now;

Suppose we introduce a new set of dependent variables Z(t ) using the transformation:

Where;

T is the n x n transformation matrix to be selected. Then we have:

Then;

where;

we have the mass and stiffness matrices in the new coordinate system

Now the question is:

Can we select such that T such that the mass and stiffness matrices in the new coordinate system are diagonal?

IF yes, then, the equation for Z(t) would represent a set of uncoupled equations and can be solved easily.

Step 5: Arriving at the Eigen value problem

Now;

Our aim is to select the Transformation matrix ‘T’ such that the equations become uncoupled in the new set of co-ordinate system- that the mass and stiffness matrices in the new coordinate system are diagonal.

To achieve this, let us assume that the equation;

Represents the equation of an undamped free vibration in which all the points on the structure oscillate harmonically at the same frequency.

That is;

where; k=1,2,....n

where 'R' is a nx1 vector and Z is the vector;

Now,

and;

Substituting this in the equation;

We have;

which implies;

Therefore;

This is a algebraic Eigen value problem because:

Mathematically, we’re looking for vectors R that solve this equation, as every positive definite matrix is invertible, any vector that solves that equation will also solve :

So then solving it is merely a task of finding the eigenvectors and respective eigenvalues. On the other hand, assuming you only have M and K, you can find multiple R and w that will satisfy this equation, assuming the matrix has a complete set of eigenvectors .

Hence R must an eigenvector of M^-1 K with eigenvalue w.

It might be worthwhile to recall the definition of Eigen values and Eigen vector at this moment:

The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector.

For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix.

The prefix eigen- is adopted from the German word "eigen" for "self" in the sense of a characteristic description. The eigenvectors are sometimes also called characteristic vectors. Similarly, the eigenvalues are also known as characteristic values.

The mathematical expression of this idea is as follows: if A is a square matrix, a non-zero vector v is an eigenvector of A if there is a scalar λ (lambda) such that;